9655. Mr. Nine and his love for mangoes
Mr.Nine was roaming
casually in the Parralel Universe in his mid-semester
breaks, suddenly he comes across a mango tree. He loves mangoes so he decides
to pluck some mangoes from it but suddenly a fairy appears and tells him to
solve a complex problem to get the mangoes. She tells him that there are n nodes in the trees, and he is given
two nodes u and v. Now she asks him how many pair of nodes are present in tree in
which shortest path between them does not contain node v after node u (for
example u → a → b → v is also
not allowed where a and b are two different nodes). If he
is able to tell the correct number of pair of nodes then he will get all the
mangoes, but he is unable to do and needs your help.
Input. The first line consists of integers n (1 ≤ n ≤ 300005),
u and v. The following n – 1
lines consist of two integers x and y denoting there is an edge between
vertices x and y (1 ≤ x, y ≤ n).
Output. Find out the total number of pair of nodes.
|
Sample
input |
Sample
ouput |
|
3 1 3 1 2 2 3 |
5 |
SOLUTION
graphs – depth frst search
Algorithm analysis
Since the input is a tree,
there is only one path between u and v. Let this path have the form: u → s
→ … → t → v. Fill the parent array so that we can find the vertices s (that follows u) and t (that comes before v).
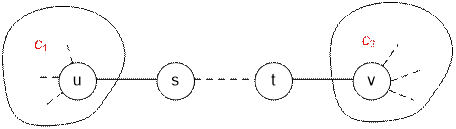
Let c1 be the number of vertices in the subtree with the
root u, provided that the edge (u, s)
is removed. Let c2 be the
number of vertices in the subtree with the root v, provided that the edge (t,
v) is removed. The number of paths
that follow u after v is c1 * c2.
The total number of paths on
the graph is n * (n – 1), where n is the number of vertices. The graph is undirected, the path from
a to b and from b to a is considered different. The number of
required pairs of vertices is
n
* (n – 1) – c1 * c2
Example
Graph from the
sample has the form:
![]()
There are 5 possible
pairs:
·
(1, 2) : path 1 → 2
·
(2, 3) : path 2 → 3
·
(3, 2) : path 3 → 2
·
(2, 1) : path 2 → 1
·
(3, 1) : path
3 → 2 → 1
Nine cannot
choose a pair (1, 3), since the shortest path between them will be 1 → 2
→ 3 and it is not acceptable, since it contains v = 3 after u
= 1, which is not acceptable.
Algorithm realization
Declare
an adjacency list of graph g and
arrays.
vector<vector<int>
> g;
vector<int>
used, parent;
The
dfs
function implements depth first search. Construct an array of ancestors parent.
void dfs(int v)
{
used[v] = 1;
for (int i =
0; i < g[v].size(); i++)
{
int to =
g[v][i];
if
(used[to] == 0)
{
parent[to] = v;
dfs(to);
}
}
}
The
dfs1
function implements depth first search from the vertex v. In the variable c1
we count the number of vertices in the subtree with the root v, provided that the transition to the
vertex s is prohibited.
void dfs1(int v)
{
used[v] = 1;
c1++;
for (int i =
0; i < g[v].size(); i++)
{
int to =
g[v][i];
if (to
== s) continue;
if
(used[to] == 0) dfs1(to);
}
}
The
dfs2
function implements depth first search from the vertex v. In the variable c2
we count the number of vertices in the subtree with the root v, provided that the transition to the
vertex t is prohibited.
void dfs2(int v)
{
used[v] = 1;
c2++;
for (int i =
0; i < g[v].size(); i++)
{
int to =
g[v][i];
if (to
== t) continue;
if
(used[to] == 0) dfs2(to);
}
}
The
main part of the program. Read the input data. Construct a graph.
scanf("%d %d %d",
&n, &start, &finish);
g.resize(n + 1);
used.resize(n + 1);
parent.resize(n + 1);
for (i = 0; i < n - 1; i++)
{
scanf("%d
%d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
Start
the depth first search from the vertex start.
dfs(start);
Using
the parent array, we find the
vertices s and t:
start → s → ... → t → finish
t = parent[finish];
s = finish;
while (parent[s] !=
start) s = parent[s];
Using
the depth first search, compute the values of c1 and c2.
c1 = 0;
used.clear(); used.resize(n + 1);
dfs1(start);
c2 = 0;
used.clear(); used.resize(n + 1);
dfs2(finish);
Print
the answer.
res = 1LL * n * (n - 1) - c1 * c2;
printf("%lld\n",
res);